15: Générer la confiance par la Théorie des Jeux

1. La confiance par la Théorie des Jeux

Comment générer la confiance quand on ne peut envoyer un message fiable (technique du Handicap) ni ne faire que répéter ce que raconte tout le monde (technique du robinet d’eau tiède) ?

Le Dilemme du Prisonnier

La modélisation des relations inter-personnelles par ce qu’on appelle la Théorie des Jeux (Wikipedia FR) a permis de répondre à cette question, notamment au travers du plus célèbre de ces “jeux” : le Dilemme du Prisonnier.

La page Wikipedia le présente ainsi :

“La forme habituelle de ce dilemme est celle de deux prisonniers (complices d’un délit) retenus dans des cellules séparées et qui ne peuvent communiquer.
si un des deux prisonniers dénonce l’autre, il est remis en liberté alors que le second obtient la peine maximale (10 ans) ;
si les deux se dénoncent entre eux, ils seront condamnés à une peine plus légère (5 ans) ;
si les deux refusent de dénoncer, la peine sera minimale (6 mois), faute d’éléments au dossier.”

En d’autres termes : la meilleure solution pour chacun est de trahir (dénoncer) l’autre et que l’autre ne le dénonce pas, les deux prisonniers vont donc faire ce choix… et ils obtiendront pire que s’ils avaient coopéré.

Cette même page Wikipedia montre un exemple d’application : 

“Ce problème modélise bien les questions de politique tarifaire : le concurrent qui baisse ses prix gagne des parts de marché et peut ainsi augmenter ses ventes et accroître éventuellement son bénéfice… mais si son concurrent principal en fait autant, les deux peuvent y perdre.”

Plus généralement, ce dilemme montre comment l’altruisme a pu se développer entre des personnes non apparentées.

Le Dilemme Itéré du Prisonnier (IDP)

La limite du Dilemme du Prisonnier est qu’elle ne concerne qu’une seule interaction. Il s’agit là d’une situation qui existe mais qui n’est pas majoritaire : nous avons généralement plus de contacts avec ceux que nous serons ammenés à revoir qu’avec les inconnus que nous ne reverrons pas. Les chercheurs ont donc imaginé ce qui se passerait si les joueurs n’avaient pas un seul coup mais au contraire un grand nombre d’échanges : c’est ce qu’on appelle le Dilemme Itéré du Prisonnier (“IDP“).

Tit-For-Tat

Robert Axelrod avait organisé en 1979 un grand tournoi pour déterminer quelle serait la meilleure stratégie dans cette situation. Pour cela, il a opposé des stratégies une à une sur un ordinateur, et compté les points, et c’est la stratégie “Tit-For-Tat” (“TFT” ou “T4T“, traduite en français par “Donnant-Donnant” ou “oeil pour oeil, dent pour dent“) qui a gagné (Axelrod, 1981 ; Axelrod & Hamilton, 1981). Elle est simplissime : “Je coopère au premier tour et je fais systématiquement comme l’autre aux tours suivants” (s’il trahit je trahis, s’il coopère je coopère aussi).

L’intérêt principal de cette stratégie est qu’elle entraîne une coopération à long terme quand elle est confrontée à elle-même, sans être désastreuse face à une stratégie plus agressive. Des améliorations ont depuis été apportées, certaines introduisant une dose supplémentaire de “pardon” (ex : Wu et Axelrod, 1995), d’autres plus réalistes exploitant mieux les coopérateurs compulsifs (ex : stratégie “Pavlov” de Nowak & Sigmund (1993), mais voir Wu et Axelrod (1995) et Wedekind & Milinski (1996)).

Application pratique

“Fool me once, shame on you; fool me twice, shame on me“
(Proverbe anglais)

La théorie des Jeux est un domaine de recherche fascinant qui ne se limite bien sûr pas au Dilemme du Prisonnier, mais celui-ci apporte déjà énormément. Il permet notamment de déterminer quelles sont les conditions qui favorisent la coopération et découragent la trahison, et tous les points trouvés sont applicables en business, les principaux étant :

• Il faut commencer par coopérer : cette prise de risque est nécessaire pour permettre de lancer le cercle vertueux. Par exemple : commencer la relation client par une publicité mensongère est, dans ce cadre, un mauvais départ.

• Conséquence du point précédent : il faut être capable de survivre à une trahison frontale (un impayé…)

• L’interaction doit être visible : il faut que chacun ait une information fiable sur les actions de l’autre, une mauvaise interprétation pouvant mener au cycle de trahison.

• Faire attention à sa réputation (les informations viennent aussi de l’extérieur de la relation)

• Faire savoir que l’on pratique le T4T

• Savoir punir… et le faire savoir

• L’interaction doit être répétée et sa fin ne doit pas être connue : le client qui est persuadé ne plus jamais avoir affaire au fournisseur pourra être tenté de ne pas payer la dernière facture… (à noter qu’il y a récursion : si la trahison au dernier tour est rentable, alors l’autre risque de trahir, donc il faut trahir  au tour d’avant, mais l’autre le sait aussi, donc …, etc., le raisonnement se poursuivant jusqu’au premier échange)

Pour aller plus loin

• Voir sur Evopsy cet extrait traduit de Hart & Aumann (2005) sur le Paradoxe du Maître Chanteur et comment être crédible (Robert Aumann a obtenu le Prix Nobel d’économie en 2005 pour ses travaux sur la Théorie des Jeux, toute cette interview est passionnante).

• Richard Dawkins fait une application extensive du dilemme du prisonnier dans son best-seller “Le Gène Egoïste“.

• Dans “Pourquoi les femmes des riches sont belles : Programmation génétique et compétition sexuelle” (pp 33-55) je détourne un peu l’approche de Dawkins pour expliquer la programmation génétique du comportement.

Photo : “Casanova once stayed here.” par Dennis Jarvis – Licence : CC BY-SA
“The basement of the Doge’s Palace contains several prison cells which housed prisoners during their interrogation and trial. Giacomo Casanova (famous as a womanizer that his name remains synonymous with the art of seduction), the palace’s most famous former prisoner, escaped from one of these cells in 1756.”

2. Toutes les Grand-Mères se valent-elles ?

“Mama’s baby, Papa’s maybe”
(Proverbe américain)

L’intérêt de l’IDP (ci-dessus) est qu’il permet d’expliquer le développement de la coopération chez des non-apparentés. Il est en effet beaucoup plus facile d’expliquer la coopération, et même l’altruisme, entre des personnes proches génétiquement : il suffit de se mettre au niveau de l’intérêt des gènes.

Inclusive Fitness

Le calcul de la proximité génétique se fait par la probabilité qu’un gène présent chez un se retrouve aussi chez l’autre. En moyenne, il y a 50% de chances entre chaque parent et un enfant, 50% aussi entre deux frères et soeurs, 25% entre grand-parents et petit-enfant, 12,5% entre cousins, etc. En d’autres termes : pour vos gènes, vous sacrifier pour 3 de vos frères ou 9 de vos cousins est rentable. Le terme employé est : “Inclusive Fitness”.

Ces chiffres ne sont en fait que des moyennes théoriques : les infidélités d’un côté et les mariages entre cousins de l’autre viennent diminuer ou augmenter les probabilités, et en plus, comme nous allons le voir, les chiffres dépendent aussi du trajet.

Le point important est que les différences de proximité génétique ont un impact sur l’altruisme. Fox et al. (2010) ont montré que les chances de survie d’un petit-enfant est lié à sa proximité génétique avec sa grand-mère, or celle-ci ne varie que de 23% à 27%.

Le calcul de Fox et al. est le suivant :

• Le chromosome X représente “environ 4.4% de notre ADN, soit  1529 gènes estimés, il contient peut-être approximativement 8% de tous les gènes humains” (Fox et al., 2010)

• Il reste (100 – 8) = 92% de gènes autosomes (ie : autres que X ou Y) qui ont 25% de probablité (1/4 chances) de se retrouver à 2 générations (grand-parent -> petit-enfant), soit 92/4 = 23%

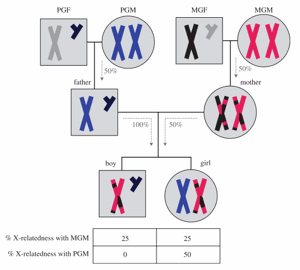
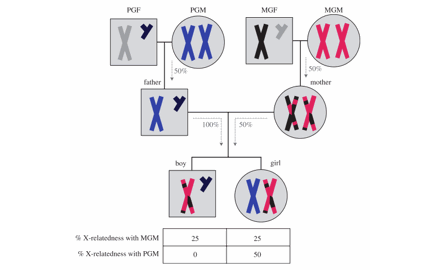
• Un petit-enfant peut avoir, en fonction de son sexe et de la lignée, entre 0 et 50% (1/2) de probabilité de porter le chromosome X de sa grand-mère (voir image ci-dessus pour comprendre), soit entre 0 et 8/2 = 4%

• La proximité génétique entre un petit-enfant et sa grand-mère est donc l’addition des deux, et va de 23% (Grand-mère Paternelle – Petit-fils : 23% + 0) à 27% (Grand-mère Paternelle – Petite-fille : 23% + 4%), et 25% pour les Grand-mères Maternelles (la moyenne globale étant bien de 25%)

Et les résultats de l’étude sont résumés sur ce tableau extrait de l’article :

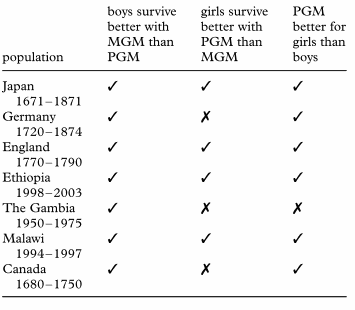
La (faible) différence de proximité génétique a bien eû un impact sur la survie.

Application pratique

Cibler la famille est un grand classique de la publicité et c’est facile à expliquer. Ce que Fox et al. ont apporté est de montrer que +/- 2 points d’écarts suffisent pour avoir un impact sur la survie dans ces populations, c’est-à-dire que l’effet est extrêmement sensible.

Se retrouve-t-il dans les quantités de cadeaux des grand-mères ? Peut-on s’en servir pour mieux cibler ses campagnes de communication ?

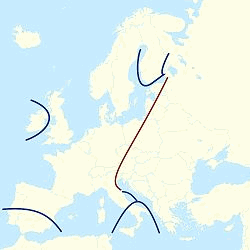
L’hypothèse est à tester mais l’effet sera certainement plus faible en Europe : l’évolution à l’ouest de la ligne de Hajnal (1985, c’est la ligne rouge sur la carte) au cours du dernier millénaire a justement sélectionné pour un plus grand altruisme hors parentèle.

Images : Fox et al. (2010), Figure 1 et Table 2 ; Carte : Wikipedia.
Légende :
- PGF : Paternal Grandfather = Grand-Père Paternel
- PGM : Paternal Grandmother = Grand-Mère Paternelle
- MGF : Maternal Grandfather = Grand-Père Maternel
- MGM : Maternal Grandmother = Grand-Mère Maternelle